লেখচিত্রের মাধ্যমে সমাধান
৭ম শ্রেণি গণিত অনুশীলনী ৭.৩ এর প্রশ্ন সমাধান
১. x/3 – 3 = 0 সমীকরণের মূল নিচের কোনটি (Which one of the following is the root of the equation x/3 - 3 = 0)?
(ক) 1/3
(খ) 3
(গ) 9
(ঘ) -9
উত্তরঃ গ
২. একটি ত্রিভুজের বাহু তিনটির দৈর্ঘ্য (x+1) সেমি, (x+2) সেমি ও (x+3) সেমি (x>0) [Length of three sides of a triangle are (x +1) cm., (x +2) cm. and ( x + 3) cm. (x > 0)]। ত্রিভুজটির পরিসীমা 15 সেমি হলে, x এর মান কত (If the perimeter of the triangle is 15 cm., what is the value of x)?
(ক) 1 সেমি
(খ) 2 সেমি
(গ) 3 সেমি
(ঘ) 6 সেমি
উত্তরঃ গ
৩. কোন সংখ্যার এক-চতুর্থাংশ 4 এর সমান হবে (What is the number of which one-fourth is equal to 4)?
(ক) 16
(খ) 12
(গ) 4
(ঘ) ¼
উত্তরঃ ক
৪. (2,-2) বিন্দুটি কোন চতুর্ভাগে অবস্থিত [In which quadrant the position of the point (2,-2)]?
(ক) প্রথম
(খ) দ্বিতীয়
(গ) তৃতীয়
(ঘ) চতুর্থ
উত্তরঃ ঘ
৫. y অক্ষ বরাবর কোন বিন্দুর ভুজ কত (What is the abscissa of the point along the Y-axis)?
(ক) 0
(খ) 1
(গ) -1
(ঘ) y
উত্তরঃ ক
৬. দুইটি সংখ্যার বিয়োগফল y, বড় সংখ্যাটি z হলে, ছোট সংখ্যাটি কত (The difference between two numbers is y, if the larger number is z, what is the smaller number)?
(ক) z-y
(খ) z+y
(গ) –y-z
(ঘ) –z+y
উত্তরঃ ক
৭. ab/xy এর সমতুল ভগ্নাংশ নিচের কোনটি (Which of the following is the equivalent fraction of ab/xy)?
(ক) abc/xyz
(খ) a2b/x2y
(গ) 2ab/2xy
(ঘ) ab2/xy2
উত্তরঃ গ
৮. 3x+1=0 সমীকরণের ঘাত কত (What is the power of the equation 3x+1= 0)?
(ক) -1/3
(খ) 1/3
(গ) 1
(ঘ) 3
উত্তরঃ গ
৯. কোন সংখ্যার সাথে -5 যোগ করলে 15 হবে (With which number does addition of-5equal to15)?
(ক) -20
(খ) 10
(গ) -10
(ঘ) 20
উত্তরঃ ঘ
১০. x এর কোন মান 4x+1=2x+7 সমীকরণকে সিদ্ধ করে (What value of x satisfies the equation of 4x +1 = 2x + 7)?
(ক) 0
(খ) 2
(গ) 3
(ঘ) 4
উত্তরঃ গ
১১. চিত্র থেকে নিচের ছকটি পূরণ কর (Fill in the following table from the given graphs):
(উভয় অক্ষে ক্ষুদ্রতম বর্গক্ষেত্রের বাহুর দৈর্ঘ্যকে একক ধরে - assuming the length of the side of the smallest square as unit along both axes)
পূরণকৃত প্রদত্ত ছকঃ
|
বিন্দু
|
স্থানাঙ্ক
|
|
A
|
(4,3)
|
|
B
|
(-2,2)
|
|
C
|
(3,-5)
|
|
D
|
(-3,-3)
|
|
O
|
(0,0)
|
|
P
|
(5,0)
|
|
Q
|
(0,4)
|
১২. নিচের বিন্দুগুলো ছক কাগজে স্থাপন করে তীর চিহ্ন অনুযায়ী যোগ কর ও চিত্রটির জ্যামিতিক নামকরণ কর (By plotting the following points on graph paper join them successively as directed by arrow-heads & give-the –geometric-name of the figures):
(ক) (2,2) 🠊 (6,2) 🠊 (6,6) 🠊 (2,6) 🠊 (2,2)
(খ) (0,0) 🠊 (-6,-6) 🠊 (8,6) 🠊 (0,0)
সমাধানঃ
(ক)
মনে করি,
পরস্পর দুইটি লম্ব রেখা XOX’ এবং YOY’ যথাক্রমে x অক্ষ এবং y অক্ষ। এবং O হচ্ছে মূলবিন্দু।ছক কাগজের ক্ষুদ্রতম বর্গের দৈর্ঘ্যকে একক ধরে (2,2), (6,2), (6,6), (2,6) বিন্দুগুলো ছক কাগজে স্থাপন করে তীর চিহ্ন অনুযায়ী যোগ করা হলো-
তাহলে, লেখচিত্রে দেখতে পাই, এটি একটি বর্গক্ষেত্রের চিত্র।
(খ)
মনে করি,
পরস্পর দুইটি লম্ব রেখা XOX’ এবং YOY’ যথাক্রমে x অক্ষ এবং y অক্ষ। এবং O হচ্ছে মূলবিন্দু।ছক কাগজের ক্ষুদ্রতম বর্গের দৈর্ঘ্যকে একক ধরে (0,0), (-6,-6), (8,6) বিন্দুগুলো ছক কাগজে স্থাপন করে তীর চিহ্ন অনুযায়ী যোগ করা হলো-
তাহলে, লেখচিত্রে দেখতে পাই, এটি একটি ত্রিভুজের চিত্র।
১৩. সমাধান কর এবং সমাধান লেখচিত্রে দেখাও (Solve and show the solutions in graphs):
(ক) x-4=0
(খ) 2x+4=0
(গ) x+3=8
(ঘ) 2x+1=x-3
(ঙ) 3x+4=5x
সমাধানঃ
(ক)
x-4=0
বা, x=4
লেখচিত্র অঙ্কনঃ
প্রদত্ত সমীকরণ, x-4=0. x এর কয়েকটি মানের জন্য x-4 এর অনুরূপ মান বের করি যেগুলোর মাধ্যমে নিচের ছকটি তৈরি করিঃ
|
x
|
x-4
|
(x,x-4)
|
|
0
|
-4
|
(0,-4)
|
|
4
|
0
|
(4,0)
|
|
8
|
4
|
(8,4)
|
লেখচিত্র অংকনের জন্য তিনটি বিন্দু (0,-4), (4,0) এবং (8,4) নেওয়া হলো।
মনে করি,
পরস্পর দুইটি লম্ব রেখা XOX’ এবং YOY’ যথাক্রমে x অক্ষ এবং y অক্ষ। এবং O হচ্ছে মূলবিন্দু।ছক কাগজের ক্ষুদ্রতম বর্গের দৈর্ঘ্যকে একক ধরে (0,-4), (4,0), (8,4) বিন্দুগুলো স্থাপন করি এবং বিন্দুগুলো সংযোগ করি।
লেখচিত্রটিতে একটা সরলরেখা পাওয়া যায়। এই সরলরেখাটি x-অক্ষকে (4,0) বিন্দুতে ছেদ করে যায়। বিন্দুটির ভুজ হচ্ছে 4। অতএব, সমীকরণটির সমাধান, x=4.
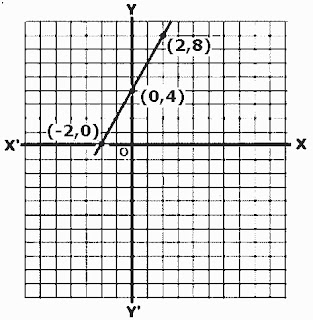
(খ)
2x+4=0
বা, 2x=-4
বা, x=-4/2
বা, x=-2
লেখচিত্র অঙ্কনঃ
প্রদত্ত সমীকরণ, 2x+4=0. x এর কয়েকটা মান নিয়ে 2x+4 এর কয়েকটা মান বের করি এবং নিচের ছকটি তৈরি করিঃ
|
x
|
x-4
|
(x,2x+4)
|
|
0
|
4
|
(0,4)
|
|
2
|
8
|
(2,8)
|
|
-2
|
0
|
(-2,0)
|
লেখচিত্র অংকনের জন্য তিনটা বিন্দু (0,-4), (2,8) এবং(-2,0) নেওয়া হলো। মনে করি,
পরস্পর দুইটি লম্ব রেখা XOX’ এবং YOY’ যথাক্রমে x অক্ষ এবং y অক্ষ। এবং O হচ্ছে মূলবিন্দু।
ছক কাগজের ক্ষুদ্রতম বর্গের দৈর্ঘ্যকে একক ধরে (0,4), (2,8),(-2,0) বিন্দুগুলো স্থাপন করি এবং বিন্দুগুলো সংযোগ করি।
লেখচিত্রটিতে একটা সরলরেখা পাওয়া যায়। এই সরলরেখাটি x-অক্ষকে (-2,0) বিন্দুতে ছেদ করে যায়। বিন্দুটির ভুজ হচ্ছে -2। অতএব, সমীকরণটির সমাধান, x=-2.
(গ)
x+3=8
বা, x=8-3
বা, x=5
লেখচিত্র অঙ্কনঃ
প্রদত্ত সমীকরণ, x+3=8 বা, x+3-8=0 বা, x-5=0. x এর কয়েকটি মান নিয়ে x-5 এর কয়েকটি মান বের করি এবং নিচের ছকটি তৈরি করিঃ
|
x
|
x-5
|
(x,x-5)
|
|
0
|
-5
|
(0,-5)
|
|
5
|
0
|
(5,0)
|
|
7
|
2
|
(7,2)
|
লেখচিত্র অংকনের জন্য তিনটি বিন্দু (0,-5), (5,0) এবং (7,2) নেওয়া হলো। মনে করি,
পরস্পর দুইটি লম্ব রেখা XOX’ এবং YOY’ যথাক্রমে x অক্ষ এবং y অক্ষ। এবং O হচ্ছে মূলবিন্দু।ছক কাগজের ক্ষুদ্রতম বর্গের দৈর্ঘ্যকে একক ধরে (0,-5), (5,0), (7,2) বিন্দুগুলো স্থাপন করি এবং বিন্দুগুলো সংযোগ করি।
লেখচিত্রটিতে একটা সরলরেখা পাওয়া যায়। এই সরলরেখাটি x-অক্ষকে (5,0) বিন্দুতে ছেদ করে যায়। বিন্দুটির ভুজ হচ্ছে 5। অতএব, সমীকরণটির সমাধান, x=5.
(ঘ)
2x+1=x-3
বা, 2x-x=-3-1
বা, x=-4
লেখচিত্র অঙ্কনঃ
প্রদত্ত সমীকরণ, 2x+1=x-3=y ধরি।
অতএব, y=2x+1 এবং y=x-3.
y=2x+1 সমীকরণের লেখের কয়েকটা বিন্দুর স্থানাঙ্ক নির্ণয় করিঃ
|
x
|
1
|
-1
|
-4
|
|
y
|
3
|
-1
|
-7
|
আবার, y=x-3 সমীকরণের লেখের কয়েকটি বিন্দুর স্থানাঙ্ক নির্ণয় করিঃ
|
x
|
2
|
-1
|
-4
|
|
y
|
-1
|
-4
|
-7
|
মনে করি,
পরস্পর দুটি লম্ব রেখা XOX’ ও YOY’ যথাক্রমে x-অক্ষ এবং y-অক্ষ। এবং O হচ্ছে মূলবিন্দু।
উভয় অক্ষে ক্ষুদ্রতম বর্গের প্রতিটি বাহুর দৈর্ঘ্যকে একক ধরি। (1,3),(-1,-1) এবং (-4,-7) বিন্দুগুলিকে লেখ কাগজে স্থাপন করে যোগ করি এবং বর্ধিত করি। তাহলে, একটা সরলরেখা পাওয়া গেল যা y=2x+1 সমীকরণটির লেখ।
আবার,
(2,-1), (-1,-4) এবং (-4,-7) বিন্দুগুলিকে লেখ কাগজে স্থাপন করি এবং যোগ করে বর্ধিত করি। তাহলে, একটা সরলরেখা পাওয়া গেল যা y=x-3 সমীকরণটির লেখ।
এই সরলরেখাটি আগের সরলরেখাটিকে A বিন্দুতে ছেদ করে। A বিন্দুটি হলো উভয় রেখার সাধারণ বিন্দু। এর স্থানাঙ্ক দুইটি সমীকরণকে সিদ্ধ করে। লেখ থেকে দেখা যায় যে, A বিন্দুর ভুজ -4.
সুতরাং, নির্ণেয় সমাধান x=-4.
(ঙ)
3x+4=5x
বা, 3x-5x=-4
বা, -2x=-4
বা, x=-4/-2
বা, x=2
লেখচিত্র অঙ্কনঃ
প্রদত্ত সমীকরণ, 3x+4=5x=y ধরি।
অতএব, y=3x+4 এবং y=5x.
y=3x+4 সমীকরণটির লেখের কয়েকটি বিন্দুর স্থানাঙ্ক নির্ণয় করিঃ
|
x
|
1
|
2
|
-2
|
|
y
|
7
|
10
|
-2
|
আবার, y=5x সমীকরণটির লেখের কয়েকতি বিন্দুর স্থানাঙ্ক নির্ণয় করিঃ
|
x
|
1
|
2
|
-1
|
|
y
|
5
|
10
|
-5
|
মনে করি,
পরস্পর দুটি লম্ব রেখা XOX’ ও YOY’ যথাক্রমে x-অক্ষ আর y-অক্ষ। এবং O মূলবিন্দু।
উভয় অক্ষে ক্ষুদ্রতম বর্গের প্রত্যেক বাহুর দৈর্ঘ্যকে একক ধরি। (1,7), (2,10) এবং (-2,-2) বিন্দুগুলিকে লেখ কাগজে স্থাপন করে যোগ করি ও বর্ধিত করি। তাহলে, একটা সরলরেখা পাওয়া গেল যা y=3x+4 সমীকরণটির লেখ।
আবার,
(1,5), (2,10) এবং (-1,-5) বিন্দুগুলিকে লেখ কাগজে স্থাপন করি ও যোগ করে বর্ধিত করি। তাহলে, একটা সরলরেখা পাওয়া গেল যা y=5x সমীকরণ এর লেখ।
এই সরলরেখা আগের সরলরেখাকে A বিন্দুতে ছেদ করে। A বিন্দু উভয় রেখার সাধারণ বিন্দু। এর স্থানাঙ্ক দুইটি সমীকরণকে সিদ্ধ করে। লেখ থেকে দেখা যায় যে, A বিন্দুর ভুজ 2.
সুতরাং, নির্ণেয় সমাধান x=2.
১৪. একটি ত্রিভুজের তিন বাহুর দৈর্ঘ্য (x+2) সেমি, (x+4) সেমি ও (x+6) সেমি (x>0) এবং ত্রিভুজটির পরিসীমা 18 সেমি (Length of three sides of a triangle are (x + 2) cm (x + 4) cm and (x + 6) cm (x > 0 & perimeter of the triangle is 18 cm)।
ক. প্রদত্ত শর্তানুযায়ী আনুপাতিক চিত্র আঁক (Draw a proportional figure by the given conditions)।
সমাধানঃ
(ক)
প্রদত্ত শর্তানুযায়ী ত্রিভুজের আনুপাতিক চিত্র আঁকা হলোঃ
(খ)
প্রশ্নমতে,
(x+2)+(x+4)+(x+6)=18
বা, 3x+12=18
বা, 3x=18-12
বা, 3x=6
বা, x=6/3
বা, x=2
(গ)
সমাধান করে পাই,
x=2
বা, x-2=0
লেখচিত্র অঙ্কনঃ
x-2=0 সমীকরণে, x এর কয়েকটি মান এর জন্য x-2 এর কয়েকটি মান বের করি এবং নিচের ছকটি তৈরি করিঃ
|
x
|
x-2
|
(x,x-2)
|
|
0
|
-2
|
(0,-2)
|
|
2
|
0
|
(2,0)
|
|
4
|
2
|
(4,2)
|
লেখচিত্র অংকনের জন্য তিনটি বিন্দু (0,-2), (2,0) ও (4,2) নেওয়া হলো। মনে করি, পরস্পর লম্ব রেখা XOX’ এবং YOY’ যথাক্রমে x-অক্ষ ও y-অক্ষ এবং O মূলবিন্দু। ছক কাগজের প্রতি এক বর্গের দৈর্ঘ্যকে একক ধরে বিন্দুগুলি স্থাপন করি এবং বিন্দুগুলি সংযোগ করি।
আমরা লেখচিত্রে একটা সরলরেখা পাই। সরলরেখাটি x অক্ষকে (2,0) বিন্দুতে ছেদ করে যায়। এখানে বিন্দুটির ভুজ হলো 2। সুতরাং প্রদত্ত সমীকরণটির সমাধান x=2।
১৫. ঢাকা ও আরিচার মধ্যবর্তী দূরত্ব 77 কিমি (Distance between Dhaka and Aricha is 77 km)। একটি বাস ঘণ্টায় 30 কিমি বেগে ঢাকা থেকে আরিচার পথে রওনা দিল (A bus started from Dhaka towards Aricha with the speed of 30 km per hour)। অপর একটি বাস ঘণ্টায় 40 কিমি বেগে আরিচা থেকে ঢাকার পথে একই সময়ে রওনা দিল (At the same time, another bus started from Aricha towards Dhaka with the speed of 40 km per hour)। বাস দুইটি ঢাকা থেকে x কিমি দূরে মিলিত হলো (The two buses meet at a distance of x k.m. from Dhaka)।
ক. বাস দুইটি আরিচা থেকে কত দূরে মিলিত হবে তা x এর মাধ্যমে প্রকাশ কর (How far from Aricha will the two buses meet, Express it in terms of x)।
সমাধানঃ
ক.
ঢাকা হতে আরিচার দূরত্ব 77 কি.মি.
ঢাকা হতে বাস দুইটির মিলন স্থানের দূরত্ব x কি.মি.
তাহলে, আরিচা হতে বাস দুইটির মিলন স্থানের দূরত্ব (77-x) কি.মি.।
খ.
১ম বাস 30 কিমি যায় 1 ঘন্টায়
∴১ম বাস 1 কিমি যায় 1/30 ঘন্টায়
∴১ম বাস x কিমি যায় x/30 ঘন্টায়
আবার,
২য় বাস 40 কিমি যায় 1 ঘন্টায়
∴২য় বাস 1 কিমি যায় 1/40 ঘন্টায়
∴২য় বাস (77-x) কিমি যায় (77-x)/40 ঘন্টায়
এখন,
বাস দুইটি একই সময় ছেড়ে যায় এবং নির্দিষ্ট সময় পর এরা মিলিত হয়।
অতএব,
x/30=(77-x)/40
বা, x✕40=30✕(77-x)
বা, x✕4=3✕(77-x) [10 দ্বারা ভাগ করে]
বা, 4x=231-3x
বা, 4x+3x=231
বা, 7x=231
বা, x=231/7
বা, x=33
গ.
১ম বাস 30 কিমি যায় 1 ঘন্টায়
∴১ম বাস 1 কিমি যায় 1/30 ঘন্টায়
∴১ম বাস 77 কিমি যায় 77/30 ঘন্টায়
এখন,
77/30 ঘণ্টা
=2 ঘন্টা+17/30 ঘণ্টা
=2 ঘন্টা + (17✕60)/30 মিনিট
=2 ঘন্টা+34 মিনিট
=2 ঘন্টা 34 মিনিট
আবার,
২য় বাস 40 কিমি যায় 1 ঘন্টায়
∴২য় বাস 1 কিমি যায় 1/40 ঘন্টায়
∴২য় বাস 77 কিমি যায় 77/40 ঘন্টায়
এখন,
77/40 ঘণ্টা
=1 ঘণ্টা+37/40 ঘণ্টা
=1 ঘণ্টা+(37✕60)/40 মিনিট
=1 ঘণ্টা+55 মিনিট+20/40 মিনিট
=1 ঘণ্টা+55 মিনিট+(20✕60)/40 সেকেন্ড
=1 ঘণ্টা+55 মিনিট+30 সেকেন্ড
=1 ঘণ্টা 55 মিনিট 30 সেকেন্ড
অতএব, গন্তব্যস্থলে পৌঁছাতে প্রথম বাসের লাগে 2 ঘন্টা 34 মিনিট এবং দ্বিতীয় বাসের লাগে 1 ঘণ্টা 55 মিনিট 30 সেকেন্ড।









No comments:
Post a Comment