নবম-দশম শ্রেণি সাধারণ গণিত - অনুশীলনী-৬.২ - রেখা, রশ্মি ও কোণ

 

রেখা, রশ্মি ও কোণ:

১. কোণের অভ্যন্তর ও বহির্ভাগের সংজ্ঞা দাও।

সমাধানঃ

কোণের অভ্যন্তরঃ

∠POQ এর অভ্যন্তর হলো OP এর Q পার্শ্বে O এবং OQ এর P পার্শ্বে অবস্থানকৃত সমতলের সকল বিন্দুর সেট।

কোণের বহির্ভাগঃ

কোণটির অভ্যন্তরে বা বাহুতে অবস্থানকৃত নয় সমতলস্থ এমন সকল বিন্দুর সেট হলো কোণের বহির্ভাগ।

কোণটির অভ্যন্তরে অবস্থিত সকল বিন্দুকে বলা হয় অন্তঃস্থ বিন্দু এবং বহির্ভাগে অবস্থিত সকল বিন্দুকে বলা হয় বহিঃস্থ বিন্দু।
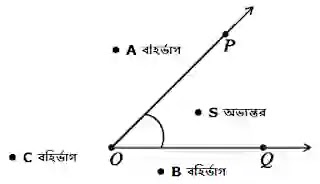
চিত্রে, S বিন্দু ∠POQ এর অভ্যন্তরে এবং  A, B, C বিন্দুগুলো ∠POQ এর বহির্ভাগে অবস্থিত।

২. যদি একই সরলরেখাস্থ তিনটি ভিন্ন বিন্দু হয়, তবে চিত্রের উৎপন্ন কোণগুলোর নামকরণ কর।

সমাধানঃ

চিত্রে উৎপন্ন কোণগুলোর নাম হলোঃ ∠DBE, ∠ABD, ∠DBC, ∠CBE, ∠EBC, ∠ABE.

উৎপন্ন কোণগুলোর নামকরণঃ

∠DBE=সরল কোণ
∠ABD=সমকোণ
∠DBC=সূক্ষ্মকোণ
∠CBE=স্থূলকোণ
∠EBC=প্রবৃদ্ধ কোণ
∠ABE=সমকোণ।

৩. সন্নিহিত কোণের সংজ্ঞা দাও এবং এর বাহুগুলো চিহ্নিত কর।

সমাধানঃ

সন্নিহিত কোণঃ

একই তলে অবস্থিত দুইটি কোণের যদি একই শীর্ষবিন্দু থাকে, একটি সাধারণ বাহু থাকে এবং তাদের অভ্যন্তরদ্বয়ে কোনো সাধারণ বিন্দু না থাকে, তবে কোণ দুইটি একে ওপরের সন্নিহিত কোণ।

চিত্রে, ∠BOA ও ∠AOC দুইটি সন্নিহিত কোণ যাদের সাধারণ বাহু OA এবং দুইটি বহিঃস্থ বাহু BO ও OC.

৪. চিত্রসহ সংজ্ঞা দাওঃ বিপ্রতীপ কোণ, পূরক কোণ, সম্পূরক কোণ, সমকোণ, সূক্ষ্মকোণ এবং স্থূলকোণ।

সমাধানঃ

নিচে চিত্রসহ, বিপ্রতীপ কোণ, পূরক কোণ, সম্পূরক কোণ, সমকোণ, সূক্ষ্মকোণ এবং স্থূলকোণের সংজ্ঞা নিচে দেওয়া হলোঃ-