নবম-দশম শ্রেণি সাধারণ গণিত - অনুশীলনী-৭.২ - চতুর্ভুজ অঙ্কন

 

চতুর্ভুজ অঙ্কন:

১. সমকোণী ত্রিভুজের সূক্ষ্মকোণের পরিমাণ দেওয়া থাকলে নিন্মের কোন ক্ষেত্রে ত্রিভুজ অঙ্কন করা সম্ভব?

ক) 60⁰ ও 36⁰   খ) 40⁰ ও 50⁰
গ) 30⁰ ও 70⁰   ঘ) 80⁰ ও 20⁰
উত্তরঃ খ

২. একটি ত্রিভুজের দুইটি বাহুর দৈর্ঘ্য যথাক্রমে 4 সেমি ও 9 সেমি হলে তৃতীয় বাহুর দৈর্ঘ্য কত সেমি?

ক) 4  খ) 5  গ) 6  ঘ) 13
উত্তরঃ গ

৩. একটি সমদ্বিবাহু সমকোণী ত্রিভুজের সমান বাহুদ্বয়ের প্রতিটির দৈর্ঘ্য 18 সেমি হলে ত্রিভুজটির ক্ষেত্রফল কত বর্গসেমি?

ক) 36  খ) 81  গ) 162  ঘ) 324
উত্তরঃ গ

৪. নির্দিষ্ট একটি চতুর্ভুজ আঁকা সম্বব যদি দেয়া থাকে-

(i) চারটি বাহু ও একটি কোণ
(ii) তিনটি বাহু ও এদের অন্তর্ভুক্ত দুইটি কোণ
(iii) দুইটি বাহু ও তিনটি কোণ
নিচের কোণটি সঠিক?
ক) i   খ)   ii  গ)  i, ii   ঘ)  i, ii ও iii
উত্তরঃ ঘ

৫. রম্বসের-

(i) চারটি বাহু পরস্পর সমান
(ii) বিপরীত কোণ সমান
(iii) কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে।
নিচের কোনটি সঠিক?
ক) i, ii  খ) i, iii  গ) ii, iii ঘ) i, ii ও iii
উত্তরঃ ঘ

চিত্রে ABCD একটি আয়তক্ষেত্র, EF=2 সেমি এবং DE=3 সেমি। এই তথ্যের আলোকে (৬-৮) নং প্রশ্নের উত্তর দাওঃ

৬. BF এর দৈর্ঘ্য কত সেমি?

ক) 1  খ) √5  গ) √13  ঘ) 5
উত্তরঃ খ

৭. AB কত সেমি?

ক) 2  খ) 2√5  গ) 5√2  ঘ) 10
উত্তরঃ খ

৮. ABCD এর ক্ষেত্রফল কত বর্গসেমি?

ক) 8√5  খ ) 20   গ) 12√5   ঘ) 32√5
উত্তরঃ ক

৯. নিন্মে প্রদত্ত উপাত্ত নিয়ে চতুর্ভুজ আঙ্কন করঃ

ক) চারটি বাহুর দৈর্ঘ্য 3 সেমি, 3.5 সেমি, 2.5 সেমি ও 3 সেমি এবং একটি কোণ 45⁰।

সমাধানঃ

বিশেষ নির্বচনঃ
দেওয়া আছে, একটি চতুর্ভুজের চারটি বাহুর দৈর্ঘ্য 3 সেমি, 3.5 সেমি, 2.5 সেমি ও 3 সেমি এবং একটি কোণ 45⁰। চতুর্ভুজটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি AM থেকে AB=a=3 সেমি অংশ কেটে নিই। A বিন্দুতে ∠BAN=∠x=45⁰ অঙ্কন করি।
2) AN থেকে AD=b=3.5 সেমি অংশ কেটে নিই।
3) B ও D বিন্দুতে c=2.5 সেমি ও d=3 সেমি ব্যাসার্ধ নিয়ে ∠BAD এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপ দুইটি পরস্পরকে C বিন্দুতে ছেদ করে।
d) B, C এবং  D, C যোগ করি; তাহলে, ABCD-ই নির্নেয় চতুর্ভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, AB=a=3 সেমি; BC=c=2.5 সেমি; CD=d=3 সেমি; AD=b=3.5 সেমি এবং ∠BAD=∠x=60⁰.  ∴ ABCD নির্নেয় চতুর্ভুজ।

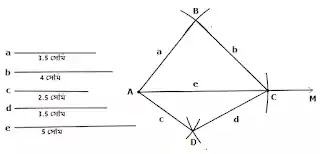
খ) চারটি বাহুর দৈর্ঘ্য 3.5 সেমি, 4 সেমি, 2.5 সেমি ও 3.5 সেমি এবং একটি কর্ণ 5 সেমি।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, একটি চতুর্ভুজের চারটি বাহুর দৈর্ঘ্য a=3.5 সেমি, b=4 সেমি, c=2.5 সেমি ও d=3.5 সেমি এবং একটি কর্ণ e=5 সেমি দেওয়া আছে। চতুর্ভুজটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) AM e=AC
2) AC এর A বিন্দুকে কেন্দ্র করে c এর সমান ব্যাসার্ধ নিয়ে এবং C কে কেন্দ্র করে d এর সমান ব্যাসার্ধ নিয়ে AC এর এক পাশে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপ দুইটি পরপ্সপরকে D বিন্দুতে ছেদ করে।
3) A, D এবং C, D যোগ করি।
4) AC এর A ও C কে কেন্দ্র করে যথাক্রমে a ও b এর সমান ব্যাসার্ধ নিয়ে D এর বিপরীত পাশে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পরকে B বিন্দুতে ছেদ করে।
5) A, B এবং C, B যোগ করি। তাহলে ABCD-ই নির্ণেয় চতুর্ভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, AB=a; AC=b; AD=c; DC=d; AC=-e; ABCD-ই নির্ণেয় চতুর্ভুজ।

গ) তিনটি বাহুর দৈর্ঘ্য 3.2 সেমি, 3 সেমি, 3.5 সেমি এবং দুইটি কর্ণ 2.8 সেমি ও 4.5 সেমি।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, একটি চতুর্ভুজের তিনটি বাহুর দৈর্ঘ্য a=3.2 সেমি, b=3 সেমি, c=3.5 সেমি এবং দুইটি কর্ণ d=2.8 সেমি ও e=4.5 সেমি দেওয়া আছে। চতুর্ভুজটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি AE থেকে a=AB অংশ কেটে নিই।
2) AB এর A ও B কে কেন্দ্র করে যথাক্রমে c ও d এর সমান ব্যাসার্ধ নিয়ে AB এর একই পাশে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পরকে D বিন্দুতে ছেদ করে।
3) A, D এবং B, D যোগ করি।
4) AB এর A ও B কে কেন্দ্র করে e ও b এর সমান ব্যসার্ধ নিয়ে একই পাশে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পরকে C বিন্দুতে ছেদ করে।
5) A, C; B, C এবং D, C যোগ করি। তাহলে ABCD-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, AB=a; AD=c; BC=b; AC=e; BD=d; ABCD-ই নির্ণেয় ত্রিভুজ।

ঘ) তিনটি বাহুর দৈর্ঘ্য 3 সেমি, 3.5 সেমি, 4 সেমি এবং দুইটি কোণ 60⁰ ও 45⁰।

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, একটি চতুর্ভুজের তিনটি বাহুর দৈর্ঘ্য a=3 সেমি, b=3.5 সেমি, c=4 সেমি এবং দুইটি কোণ x=60⁰ ও y=45⁰ দেওয়া আছে। চতুর্ভুজটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি AE থেকে c=AB অংশ কেটে নিই।
2) AB এর A বিন্দুতে x=∠BAD এবং B নিন্দুতে y=∠ABC আঁকি।
3) AD=b; BC=a অংশ কেটে নিই।
4) C, D যোগ করি। তাহলে, ABCD-ই নির্ণেয় চতুর্ভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, AB=c; AD=b; BC=a; x=∠BAD; y=∠ABC; ABCD-ই নির্ণেয় চতুর্ভুজ।

১০. নিন্মে প্রদত্ত উপাত্ত নিয়ে সামন্তরিক অঙ্কন করঃ

ক) দুইটি কর্ণের দৈর্ঘ্য 4 সেমি, 6.5 সেমি এবং এদের অন্তর্ভুক্ত কোণ 45⁰।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, একটি সমন্তরিকের দুইটি কর্ণের দৈর্ঘ্য a=4 সেমি, b=6.5 সেমি এবং এদের অন্তর্ভুক্ত কোণ x=45⁰ দেওয়া আছে। সামন্তরিকটি আঁকতে হবে।
অঙ্কনের বিবরনঃ
1) যেকোনো রশ্মি AM থেকে a=AC অংশ কেটে নিই।
2) AC এর মধ্যবিন্দু O নির্ণয় করি।
3) O বিন্দুতে x=∠AOP অঙ্কন করি এবং OP কে বিপরীত দিকে Q পর্যন্ত করি।
4) PQ থেকে OB=b/2 এবং OD=b/2 অংশ কেটে নিই।
5) B, A; B, C: C, D; A, D যোগ করি; তাহলে, ABCD-ই নির্ণেয় সামন্তরিক।
প্রমাণঃ
অঙ্কন অনুসারে, AC=a; BO+OD=b/2+b/2=b; ∠AOB=45⁰. ABCD-ই নির্ণেয় সামন্তরিক।

খ) একটি বাহুর দৈর্ঘ্য 4 সেমি এবং দুইটি কর্ণের দৈর্ঘ্য 5 সেমি, 6.5 সেমি।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, একটি সামন্তরিকের একটি বাহুর দৈর্ঘ্য c=4 সেমি এবং দুইটি কর্ণের দৈর্ঘ্য a=5 সেমি, b=6.5 সেমি দেওয়া আছে।
অঙ্কনের বিবরণঃ
1) AX c=AB
2) AB এর A ও B কে কেন্দ্র করে যথাক্রমে a/2 ও b/2 এর সমান ব্যাসার্ধ নিয়ে AB এর এক পাশে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে।
3) A, O যোগ করে E পর্যন্ত এবং B, O যোগ করে F পর্যন্ত বর্ধিত করি।
4) OC=a/2; OD=b/2 অংশ কেটে নিই।
5) A, D; D, C; C, B যোগ করি। তাহলে, ABCD নির্ণেয় সামন্তরিক।
প্রমাণঃ
অঙ্কন অনুসারে, AC=AO+OC=a/2+a/2=a; BD=BO+OD=b/2+b/2=b; AB=c; ABCD নির্ণেয় সামন্তরিক।

১১. ABCD চতুর্ভুজের AB ও BC বাহু এবং ∠B, ∠C  ও ∠D কোণ দেওয়া আছে। চতুরভুজটি আঁক।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD চতুর্ভুজের AB=a ও BC=b বাহু এবং ∠B, ∠C  ও ∠D কোণ দেওয়া আছে। চতুরভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি AE থেকে AB=a অংশ কেটে নিই।
2) B বিন্দুতে ∠ABG=∠B আঁকি।
3) BG থেকে BC=b অংশ কেটে নিই।
4) C বিন্দুতে ∠BCG=∠C আঁকি।
5) CH এর উপর একটি বিন্দু M নিই।
6) M বিন্দুতে ∠CMN=∠D আঁকি যা AB কে N বিন্দুতে ছেদ করে।
7) A বিন্দু দিয়ে NM এর সমান্তরাল করে AF আঁকি যা CH কে D বিন্দুতে ছেদ করে। তাহলে ABCD-ই নির্ণেয় চতুর্ভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, AB=a; Bc=b; ∠ABC=∠B; ∠BCD=∠C; ∠CDA=∠CMN=∠D; ABCD ABCD- নির্ণেয় চতুর্ভুজ।

১২. ABCD চতুর্ভুজের কর্ণ দুইটির ছেদবিন্দু দ্বারা কর্ণ দুইটির চারটি খন্ডিত অংশ এবং এদের অন্তর্ভুক্ত একটি কোণ যথাক্রমে OA=4 সেমি, OB=5 সেমি, OC=3.5 সেমি, OD=4.5 সেমি ও ∠AOB=80⁰ দেওয়া আছে। চতুর্ভুজটি আঁক।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD চতুর্ভুজের কর্ণ দুইটির ছেদবিন্দু দ্বারা কর্ণ দুইটির চারটি খন্ডিত অংশ এবং এদের অন্তর্ভুক্ত একটি কোণ যথাক্রমে OA=4 সেমি, OB=5 সেমি, OC=3.5 সেমি, OD=4.5 সেমি ও ∠AOB=80⁰ দেওয়া আছে। চতুর্ভুজটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রেখাংশ FH নিই।
2) FH এর উপর একটি বিন্দু O নিই।
3) O বিন্দুতে ∠BOA=80⁰=∠FOE আঁকি এবং EO কে G পর্যন্ত বর্ধিত করি।
4) OF থেকে OB; OH থেকে OD; OE থেকে OA; OG থেকে OC অংশ কেটে নিই।
5) B, C; C, D; D, A; A, B যোগ করি। তাহলে, ABCD-ই অঙ্কিত চতুর্ভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, ∠BOA=80⁰, AO=4 সেমি; OC=3.5 সেমি; BO=5 সেমি; OD=4.5 সেমি; ABCD-ই নির্ণেয় চতুর্ভুজ।

১৩. রম্বসের একটি বাহুর দৈর্ঘ্য 3.5 সেমি ও একটি কোণ 45⁰; রম্বসটি আঁক।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, রম্বসের একটি বাহুর দৈর্ঘ্য a=3.5 সেমি ও একটি কোণ x=45⁰; রম্বসটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি AE থেকে AB=a অংশ কেটে নিই।
2) AB এর A বিন্দুতে x এর সমান করে ∠BAF আঁকি।
3) AF থেকে AD=a অংশ কেটে নিই।
4) D ও B বিন্দুকে কেন্দ্র করে a এর সমান ব্যাসার্ধ নিয়ে ∠BAD এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপ দুটি পরস্পরকে C বিন্দুতে ছেদ করে।
5) D, C; B, C যোগ করি। ABCD-ই নির্ণেয় রম্বস।
প্রমাণঃ
অঙ্কন অনুসারে, AB=BC=CD=AD=a; ∠BAD=x; ABCD-ই নির্ণেয় রম্বস।

১৪. রম্বসের একটি বাহু ও একটি কর্ণের দৈর্ঘ্য দেওয়া আছে। রম্বসটি আঁক।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, রম্বসের একটি বাহু a ও একটি কর্ণের দৈর্ঘ্য b দেওয়া আছে। রম্বসটি আঁকতে হবে।
অঙ্কণের বিবরণঃ
1) যেকোনো রশ্মি AE থেকে AC=b অংশ কেটে নিই।
2) A ও C কে কেন্দ্র করে AC এর উভয় পাশে a এর সমান ব্যাসার্ধ নিয়ে দুইটি করে বৃত্তচাপ আঁকি। উভয় পাশের বৃত্তচাপদ্বয় পরস্পরকে D ও B বিন্দুতে ছেদ করে।
3) A, D; C, D; A, B; C, B যোগ করি। ABCD নির্ণেয় রম্বস।
প্রমাণঃ
অঙ্কন অনুসারে, AB=a; BC=a; CD=a; AD=a; AC=b; ABCD নির্ণেয় রম্বস।

১৫. রম্বসের দুইটি কর্ণের দৈর্ঘ্য দেওয়া আছে। রম্বসটি আঁক।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, রম্বসের দুইটি কর্ণের দৈর্ঘ্য a ও b দেওয়া আছে। রম্বসটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি AE থেকে AC=b অংশ কেটে নিই।
2) AC এর লম্ব সমদ্বিখন্ডক GH আঁকি যা AC কে O বিন্দুতে ছেদ করে।
3) OG থেকে OB=a/2 অংশ এবং OH থেকে OD=a/2 অংশ কেটে নিই।
4) A, B; B, C; C, D; D, A যোগ করি। তাহলে ABCD-ই নির্ণেয় রম্বস।
প্রমাণঃ
অঙ্কন অনুসারে, △AOB ও △COB এর মধ্য,
AO=OC; OB সাধারণ বাহু।  ∠AOB=∠COB=90⁰ [OB⊥AC]
তাহলে, △AOB ≅ △COB
∴ AB=BC
একইভাবে, AB=BC=CD=DA; AC=b; BD=BO+OD=a/2+a/2=a; ABCD-ই নির্ণেয় রম্বস।

১৬. বর্গক্ষেত্রের পরিসীমা দেওয়া আছে। বর্গক্ষেত্রটি আঁক।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, বর্গক্ষেত্রের পরিসীমা P দেওয়া আছে। বর্গক্ষেত্রটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) পরিসীমা P এর এক চতুরাংশ a নির্ণয় করি।
2) যেকোনো রশ্মি BE থেকে BC=a অংশ কেটে নিই।
3) B বিন্দুতে BE এর উপর BF লম্ব আঁকি।
4) BF থেকে BA=a অংশ কেটে নিই।
5) A ও C কে কেন্দ্র করে a এর সমান ব্যাসার্ধ নিয়ে ∠CBA এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপ দুটি পরস্পরকে D বিন্দুতে ছেদ করে।
6) A, D; D, C যোগ করি। ABCD-ই নির্ণেয় বর্গ।
প্রমাণঃ
অঙ্কন অনুসারে, BC=a; CD=a; AD=a; a+a+a+a=P; ∠CBA=90⁰। ABCD-ই নির্ণেয় বর্গ।

১৭. একটি সমকোণী ত্রিভুজের অতিভুজ 5 সেমি ও এক বাহুর দৈর্ঘ্য 4 সেমি। উপরের তথ্যের আলোকে নিচের প্রশ্নগুলোর উত্তর দাওঃ

ক) ত্রিভুজটির অপর বাহুর দৈর্ঘ্য কত?

সমাধানঃ

মনে করি, অপর বাহুর দৈর্ঘ্য x সেমি।
সুতরাং পিথাগোরাসের উপপাদ্য উপপাদ্য অনুসারে পাই,
5²=4²+x²
বা,  25=16+x²
বা,  x²=25-16
বা,  x²=9
বা,  x=3
∴অপর বাহুর দৈর্ঘ্য=3 সেমি।

খ) ত্রিভুজটি অঙ্কন কর। (অঙ্কনের চিহ্ন আবশ্যক)

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, একটি সমকোণী ত্রিভুজের অতিভুজ a=5 সেমি ও এক বাহুর দৈর্ঘ্য b=4 সেমি। ত্রিভুজটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি CX থেকে AB=b অংশ কেটে নিই।
2) CA এর C বিন্দুতে CY লম্ব আঁকি।
3) A বিন্দুতে a এর সমান একটি বৃত্তচাপ আঁকি যা CY কে B বিন্দুতে ছেদ করে।
4) A, B যোগ করি। ABC-ই নির্ণেয় ত্রিভুজ।

গ) ত্রিভুজটির পরিসীমার সমান পরিসীমাবিশিষ্ট একটি বর্গ অঙ্কন কর। (অঙ্কনের চিহ্ন আবশ্যক)

সমাধানঃ

ক হতে, ত্রিভুজের পরিসীমা=5+4+3=12 সেমি।
শর্তমতে, বর্গের পরিসীমা=12 সেমি।
তাহলে, বর্গের এক বাহুর দৈর্ঘ্য=12/4=3 সেমি।
মনে করি, কোনো বর্গের এক বাহুর দৈর্ঘ্য m=3 সেমি দেওয়া আছে। বর্গটি আঁকতে হবে।

অঙ্কনের বিবরণঃ

1) যেকোনো রশ্মি AX থেকে AB=m অংশ কেটে নিই।
2) AB এর উপর A বিন্দুতে AE লম্ব আঁকি।
3) AE থেকে AD=m অংশ কেটে নিই।
4) D ও B বিন্দুতে m এর সমান ব্যাসার্ধ নিয়ে ∠BAD এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পরকে C বিন্দুতে ছেদ করে।
5) D, C; C, B যোগ করি। তাহজলে ABCD-ই নির্ণেয় বর্গ।

১৮. ABCD চতুর্ভুজের AB=4 সেমি, BC=5 সেমি, ∠A=85⁰, ∠B=80⁰ এবং ∠C=95⁰। উপরের তথ্যের আলোকে নিচের প্রশ্নগুলোর উত্তর দাও।

ক) ∠D এর মান নির্ণয় কর।

সমাধানঃ

দেওয়া আছে, ∠A=85⁰, ∠B=80⁰ এবং ∠C=95⁰
আমরা জানি, চতুর্ভুজের চার কোণের সমষ্টি=2 সরলকোণ
∴ ∠A+∠B+∠C+∠D=360⁰
বা,  85⁰+80⁰+95⁰+∠D=360⁰
বা,  260⁰+∠D=360⁰
বা,  ∠D=360⁰-260⁰
বা,  ∠D=100⁰

খ) প্রদত্ত তথ্য অনুযায়ী ABCD চতুর্ভুজটি অঙ্কন কর। (অঙ্কনের চিহ্ন আবশ্যক)

সমাধানঃ

মনে করি, ABCD চতুর্ভুজের AB=4 সেমি, BC=5 সেমি, ∠A=85⁰, ∠B=80⁰ এবং ∠C=95⁰ দেওয়া আছে। চতুর্ভুজটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি BX থেকে BC=b অংশ কেটে নিই।
2) C বিন্দুতে ∠C এর সমান করে ∠BCF আঁকি।
3) B বিন্দুতে ∠B এর সমান করে ∠CBE আঁকি।
4) BF থেকে BA=a অংশ কেটে নিই।
5) A বিন্দুতে ∠A এর সমান করে ∠BAG আঁকি।
6) AG, CF পরস্পপরকে D বিন্দুতে ছেদ করে; তাহলে ABCD-ই নির্ণেয় চতুর্ভুজ।

গ) প্রদত্ত বাহু দুইটিকে একটি সামন্তরিকের বাহু এবং ∠B=80⁰ ধরে সামন্তরিকটি অঙ্কন কর। (অঙ্কণের চিহ্ন আবশ্যক)

সমাধানঃ

মনে করি, ABCD সামন্তরিকের দুইটি সন্নিহিত বাহু AB=4 সেমি=a; BC=5 সেমি=b এবং তাদের অন্তর্ভুক্ত কোণ ∠B=80⁰ দেওয়া আছে। সামন্তরিকটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি BX থেকে BC=b অংশ কেটে নিই।
2) B বিন্দুতে ∠B এর সমান করে ∠CBE আঁকি।
3) BE থেকে BA=a অংশ কেটে নিই।
4) A ও C কে কেন্দ্র করে যথাক্রমে b ও a এর সমান ব্যাসার্ধ নিয়ে ∠CBA এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পরকে D বিন্দুতে ছেদ করে।
5) A, D; C, D যোগ করি। তাহলে ABCD ই নির্ণেয় সামন্তরিক।

১৯. একটি ট্রাপিজিয়ামের সমান্তরাল দুইটি বাহুর দৈর্ঘ্য 4 সেমি ও 6 সেমি এবং বৃহত্তম বাহু সংলগ্ন দুইটি কোণ ∠x=60⁰ এবং ∠y=50⁰।

ক) প্রদত্ত তথ্যগুলো চিত্রের মাধ্যমে প্রকাশ কর।

সমাধানঃ

প্রদত্ত তথ্যের চিত্রঃ

খ) ট্রাপিজিয়ামটি আঁক। (অঙ্কনের চিহ্ন ও বিবরণ আবশ্যক)

সমাধানঃ

মনে করি, একটি ট্রাপিজিয়ামের দুইটি সমান্তরাল বাহুর দৈর্ঘ্য a=6 সেমি ও b=4 সেমি এবং বৃহত্তম বাহু সংলগ্ন দুইটি কোণ ∠x=60⁰ এবং ∠y=50⁰ দেওয়া আছে, ট্রাপিজিয়ামটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি AX থেকে AB=aঅংশ কেটে নিই।
2) AB এর A বিন্দুতে ∠BAY=∠x এবং  B বিন্দুতে ∠ABZ=∠y আঁকি।
3) AB থেকে AE=b অংশ কেটে নিই।
4) E বিন্দুতে ∠BEC=∠x আঁকি।
5) EC, BZ কে C বিন্দুতে ছেদ করে।
6) C বিন্দু দিয়ে CD।।AB আঁকি।
7) CD, AY কে D বিন্দুতে ছেদ করে; তাহলে, ABCD ই নির্ণেয় ট্রাপিজিয়াম।

গ) উদ্দীপকের বাহু দুইটিকে সামন্তরিকের দুইটি কর্ণ ও ∠y কে অন্তর্ভুক্ত কোণ বিবেচনা করে সামন্তরিকটি আঁক। (অঙ্কণের চিহ্ন ও বিবরণ আবশ্যক)

সমাধানঃ

মনে করি, একটি সামন্তরিকের দুইটি কর্ণের দৈর্ঘ্য যথাক্রমে a=4 সেমি ও b=6 সেমি এবং এদের অন্তর্ভুক্ত কোণ ∠y=50⁰ দেওয়া আছে। সামন্তরিকটি আঁকতে হবে।
অঙ্কনের বিবরণঃ
1) যেকোনো রশ্মি AM থেকে AC=a অংশ কেটে নিই।
2) AC এর মধ্যবিন্দু O নির্ণয় করি।
3) O বিন্দুতে ∠AOP=∠y আঁকি।
4) OP এর বিপরীত রশ্মি OQ আঁকি।
5) OP থেকে OB=b/2 অংশ এবং  OQ থেকে OD=b/2 অংশ কেটে নিই।
6) B, A; A, D; D, C; C, B যোগ করি। তাহলে, ABCD-ই নির্ণেয় সামন্তরিক।