নবম-দশম শ্রেণি সাধারণ গণিত - অনুশীলনী-৭.১ - ত্রিভুজ অঙ্কন

 

ত্রিভুজ অঙ্কন:

১. নিন্মে প্রদত্ত উপাত্ত নিয়ে ত্রিভুজ অঙ্কন করঃ

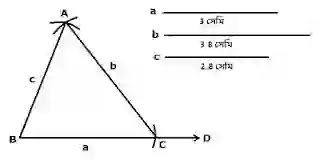
ক) তিনটি বাহুর দৈর্ঘ্য যথাক্রমে 3 সেমি, 3.5 সেমি, 2.8 সেমি।

সমাধানঃ

মনে করি, কোনো ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য যথাক্রমে a=3 সেমি, b=3.8 সেমি, c=2.8 সেমি দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ

(১) যেকোনো রশ্মি BD থেকে BC=a কেটে নিই।
(২) B, C কে কেন্দ্র করে যথাক্রমে c ও b এর সমান ব্যাসার্ধ নিয়ে BC এর একই দিকে দুইটি বৃত্তচাপ আঁকি।
(৩) মনে করি, বৃত্তচাপদ্বয় পরস্পরকে A বিন্দুতে ছেদ করে।
(৪) A, C ও B, C যোগ করি; তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কনানুসারে, AB=c, BC=a, AC=b. △ABC-ই নির্ণেয় ত্রিভুজ।

খ) দুইটি বাহুর দৈর্ঘ্য 4 সেমি, 3 সেমি এবং অন্তর্ভুক্ত কোণ 60⁰।

সমাধানঃ

মনে করি, কোনো ত্রিভুজের দুইটি বাহুর দৈর্ঘ্য a=4 সেমি, b=3 সেমি এবং অন্তর্ভুক্ত কোণ ∠x=60⁰ দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ

১) যেকোনো রশ্মি BD থেকে a এর সমান করে BC অংশ কেটে নিই।
২) BC এর B বিন্দুতে ∠x এর সমান করে ∠CBE আঁকি।
৩) BE থেকে b=BA কেটে নিই।
৪) A, C যোগ করি; তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কনানুসারে, BC=a; BA=b; ∠CBA=∠x; △ABC-ই নির্ণেয় ত্রিভুজ।

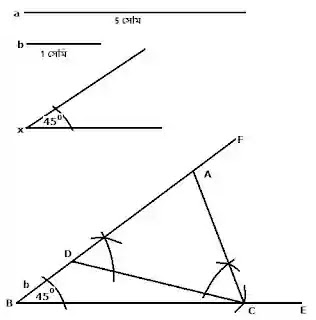
গ) দুইটি কোন 60⁰ ও 45⁰ এবং এদের সংলগ্ন বাহুর দৈর্ঘ্য 5 সেমি।

সমাধানঃ

মনে করি, একটি ত্রিভুজের দুইটি কোণ x=60⁰ ও y=45⁰ এবং এদের সংলগ্ন বাহু a=5 সেমি দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ

১) BD রেখাংশ থেকে a=BC অংশ কেটে নিই।
২) BC এর  B বিন্দুতে x=∠CBE ও  C বিইন্দুতে y=∠BCF আঁকি।
৩) BE ও CF পরস্পরকে A বিন্দুতে ছেদ করে; তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কনানুসারে, x=∠CBA ; y=∠BCA; BC=a; △ABC-ই নির্ণেয় ত্রিভুজ।

ঘ) দুইটি কোণ 60⁰ ও 45⁰ এবং 45⁰ কোণের বিপরীত বাহুর দৈর্ঘ্য 5 সেমি।

সমাধানঃ

মনে করি, একটি ত্রিভুজের দুইটি কোণ x=60⁰, y=45⁰, y কোণের বিপরীত বাহুর দৈর্ঘ্য a=5 সেমি দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ

১) BD যেকোনো রেখাংশ থেকে a=BC অংশ কেটে নিই।
২) BC এর B ও C বিন্দুতে x এর সমান করে ∠CBE ও ∠DCF আঁকি।
৩) আবার, C বিন্দুতে y এর সমান করে ∠FCA আঁকি যার CA, BF কে A বিন্দুতে ছেদ করে। তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কনানুসারে, BE।।CF (কারণ,∠DCF=∠CBE) বলে, y=∠FCA=∠BAC=45⁰. 45⁰ এর বিপরীত বাহু BC=5 সেমি।  ∠CBA=60⁰. △ABC-ই নির্ণেয় ত্রিভুজ।

ঙ) দুইটি বাহুর দৈর্ঘ্য যথাক্রমে 4.5 সেমি ও 3.5 সেমি এবং দ্বিতীয় বাহুর বিপরীত কোণ 30⁰।

সমাধানঃ

মনে করি, একটি ত্রিভুজের দুইটি বাহুর দৈর্ঘ্য a=4.5 সেমি ও b=3.5 সেমি এবং b বাহুর বিপরীত কোণ x=30⁰ দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ

১) যেকোনো রেখাংশ BD নিই।
২) BD এর B বিন্দুতে x=∠DBE আঁকি।
৩) BE থেকে a=BA অংশ কেটে নিই।
৪) A কে কেন্দ্র করে একটি বৃত্তচাপ আঁকি যা BD কে C ও C’ বিন্দুতে ছেদ করে।
৫) C ও A এবং C’ ও A যোগ করি। তাহলে, △ABC বা △ABC’-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, x=∠CBA বা ∠C’BA; a=AB; b=AC=AC’; △ABC বা △ABC’-ই নির্ণেয় ত্রিভুজ।

চ) সমকোণী ত্রিভুজের অতিভুজ ও একটি বাহুর দৈর্ঘ্য যথাক্রমে 6 সেমি ও 4 সেমি।

সমাধানঃ

মনে করি, একটি সমকোণী ত্রিভুজের অতিভুজ a=6 সেমি ও একটি বাহুর দৈর্ঘ্য b=4 সেমি দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ
১) যেকোনো রেখাংশ BD নিই।
২) BD এর B বিন্দুতে BE লম্ব আঁকি।
৩) BE থেকে b=BA অংশ কেটে নিই।
৪) A বিন্দুকে কেন্দ্র করে a এর সমান ব্যসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা BD কে C বিন্দুতে ছেদ করে।
৫) A, C যোগ করি; তাহলে △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, AB⊥BC; a=AC=অতিভুজ; b=BA; △ABC-ই নির্ণেয় ত্রিভুজ।

২. নিন্মে প্রদত্ত উপাত্ত নিয়ে ত্রিভুজ অঙ্কন করঃ

ক) ভূমি 3.5 সেমি, ভূমি সংলগ্ন একটি কোণ 60⁰ ও অপর দুই বাহুর সমষ্টি 8 সেমি।

সমাধানঃ

মনে করি, একটি ত্রিভুজের ভূমি a=3.5 সেমি ও ভূমি সংলগ্ন একটি কোণ x=60⁰ এবং অপর দুই বাহুর সমষ্টি s=8 সেমি দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ

১) যেকোনো রেখাংশ BE থেকে a=BC অংশ কেটে নিই।
২) BC এর B বিন্দুকে কেন্দ্র করে x এর সমান করে ∠CBF আঁকি।
৩) BF থেকে s=BD অংশ কেটে নিই।
৪) C, D যোগ করি।
৫) CD এর C বিন্দুতে ∠ADC=∠DCA আঁকি।
৬) ∠DCA এর CA বাহু BD কে A বিন্দুতে ছেদ করে; তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।

প্রমাণঃ
△ACD-এ ∠ADC=∠DCA, তাহলে, AC=AD
∴ s=BA+AD=BA+AC এবং BC=a; ∠CBA=x. △ABC-ই নির্ণেয় ত্রিভুজ।

খ) ভূমি 5 সেমি, ভূমি সংলগ্ন একটি কোণ 45⁰ ও অপর দুই বাহুর অন্তর 1 সেমি।

সমাধানঃ

মনে করি, একটি ত্রিভুজ যার ভূমি a=5 সেমি, ভূমি সংলগ্ন একটি কোণ x=45⁰ এবং অপর দুই বাহুর অন্তর b=1 সেমি দেওয়া আছে। ত্রিভূজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ

১) যেকোনো রেখাংশ BE থেকে a=BC অংশ কেটে নিই।
২) BC এর B বিন্দুতে x= ∠CBF আঁকি।
৩) BF থেকে b=BD লই এবং D, C যোগ করি।
৪) D বিন্দুতে উৎপন্ন ∠CDF এর সমান করে একটি কোণ  ∠DCA, C বিন্দুতে আঁকি যা BF কে  A বিন্দুতে ছেদ করে। তাহলে,  △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, △DCA এ ∠CDA=∠DCA, তাহলে, AD=AC.
∴ b=BD=AB-AD=AB-AC [AB, AC নির্ণেয় ত্রিভুজের দুই বাহু]
a=BC; x=∠CBA; △ABC-ই নির্ণেয় ত্রিভুজ।

গ) ভূমি সংলগ্ন কোণ দুইটি যথাক্রমে 60⁰ ও 45⁰ ও পরিসীমা 12 সেমি।

সমাধানঃ

মনে করি, একটি ত্রিভুজের দুইটি কোণ x=60⁰, y=45⁰ এবং এর পরিসীমা p=12 সেমি দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ
১) যেকোনো রেখাংশ DF থেকে p এর সমান করে DE অংশ কেটে নিই।
২) DE এর D বিন্দুতে  x কোণের অর্ধেকের সমান করে ∠EDH আঁকি এবং E বিন্দুতে  y এর অর্ধেকের সমান করে ∠DEG আঁকি।
৩) DH ও EG পরস্পর A বিন্দুতে ছেদ করে।
৪) A বিন্দুতে ∠DAB=∠EDA  এবং ∠EAC=∠DEA আঁকি যা DF কে B, C বিন্দুতে ছেদ করে। তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, ∠CBA=∠ADB+∠DAB=x/2+x/2=x; একইভাবে, ∠ACB=y.
এবং, AB+BC+AC=DB+BC+CE [AB=DB; AC=CE কারন এদের বিপরীত কোণদ্বয় সমান]
                             =DE=p        ; △ABC-ই নির্ণেয় ত্রিভুজ।

৩.  একটি ত্রিভুজের ভূমি সংলগ্ন দুইটি কোণ এবং শীর্ষ থেকে ভূমির উপর অঙ্কিত লম্বের দৈর্ঘ্য দেওয়া আছে। ত্রিভুজটি আঁক।

সমাধানঃ

মনে করি, একটি ত্রিভুজের ভূমি সংলগ্ন দুইটি কোণ x ও y এবং শীর্ষ থেকে ভূমির উপর অঙ্কিত লম্ব d দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ
১) যেকোনো রেখাংশ MN এর D বিন্দুতে d এর সমান করে DA লম্ব আঁকি।
২) A বিন্দু দিয়ে MN এর সমান্তরাল PQ আঁকি।
৩) A বিন্দুতে x=∠PAB এবং y=∠QAC আঁকি যার বাহু MN কে B ও C বিন্দুতে ছেদ করে। তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, PQ।।MN; AB তাদের ছেদক; তাহলে, ∠PAB=∠ABC=x
একইভাবে, ∠QAC=∠BCA=y; AD=d; △ABC-ই নির্ণেয় ত্রিভুজ।

৪. সমকোণী ত্রিভুজের অতিভূজ ও অপর দুই বাহুর সমষ্টি দেওয়া আছে। ত্রিভুজটি আঁক।

সমাধানঃ

মনে করি, একটি সমকোণী ত্রিভুজের অতিভুজ a এবং অপর দুই বাহুর সমষ্টি b দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ
১) যেকোনো রেখাংশ PQ থেকে b এর সমান করে PC কেটে নিই।
২) PC এর P বিন্দুতে 45⁰ =∠CPR আঁকি।
৩) C কে কেন্দ্র করে PR এর উপর একটি বৃত্তচাপ আঁকি যা PR কে A’ ও A বিন্দুতে ছেদ করে।
৪) C, A এবং C, A’ যোগ করি।
৫) A’ ও A থেকে PC এর উপর যথাক্রমে A’B’ ও AB লম্ব আঁকি; তাহলে, △ABC ও △A’B’C ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, △PA’B’ এ
 ∠PB’A’=90⁰; ∠B’PA’=45⁰
তাহলে, ∠PA’B’=45⁰
∴A’B’=PB”
একইভাবে, AB=PB
এখন, △ABC ও △A’B’C এ
a=AC=A’C; AB+BC=PB+BC=PC=b; A’B’+B’C=PB’+B’C=PC=b; লম্ব=AB ও A’B’; △ABC ও △A’B’C ই নির্ণেয় ত্রিভুজ।

৫. ত্রিভুজের ভূমি সংলগ্ন একটি কোণ, উচ্চতা ও অপর দুই বাহুর সমষ্টি দেওয়া আছে। ত্রিভুজটি আঁক।

সমাধানঃ

মনে করি, একটি ত্রিভুজের ভূমি সংলগ্ন একটি কোণ x; উচ্চতা h; এবং অপর দুই বাহুর সমষ্টি a দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ
১) যেকোনো রশ্মি BE নিই।
২) B বিন্দুতে x কোণের সমান ∠EBG আঁকি।
৩) BG থেকে a=BF অংশ কেটে নিই।
৪) B বিন্দুতে লম্ব BQ আঁকি।
৫) BQ থেকে b=BD অংশ কেটে নিই।
৬) D বিন্দুতে DH লম্ব আঁকি যা BF কে A বিন্দুতে ছেদ করে।
৭) A কে কেন্দ্র AF এর সমান করে BE এর উপর একটি বৃত্তচাপ আঁকি যা BE কে C’ ও C  বিন্দুতে ছেদ করে।
৮) A, C; A, C’ যোগ করি। তাহলে, △ABC’ ও △ABC ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, ∠ABC=x; BD=h; AB+AC=AB+AF=BF=a; AB+AC’=AB+AF=BF=a. △ABC’ ও △ABC ই নির্ণেয় ত্রিভুজ।

৬. সমবাহু ত্রিভুজের পরিসীমা দেওয়া আছে। ত্রিভুজটি আঁক।

সমাধানঃ

মনে করি একটি সমবাহু ত্রিভুজের পরিসীমা a দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ
১) যেকোনো রশ্মি DF থেকে p=DE কেটে নিই।
২) DE কে সমান তিন ভাবে ভাগ করি যেন DP=PQ=QE হয়।
৩) যেকোনো রশ্মি BH থেকে DP=BC নিই।
৪) BC এর B ও C বিন্দুকে কেন্দ্র করে BC এর একই পার্শ্বে DP এর সমান ব্যাসার্ধ নিয়ে দুইটি বৃতচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পরকে A বিন্দুতে ছেদ করে।
৫) A, B; A, C যোগ করি। তাহলে, △ABC ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, AB=BC=AC=DP
∴ AB+BC+AC=3DP=p; △ABC ই নির্ণেয় ত্রিভুজ।

৭. ত্রিভুজের ভূমি, ভূমি সংলগ্ন একটি স্থুলকোণ ও অপর দুই বাহুর অন্তর দেওয়া আছে। ত্রিভুজটি আঁক।

সমাধানঃ

মনে করি, একটি ত্রিভুজের ভূমি সংলগ্ন স্থুলকোণ x ও অপর দুই বাহুর অন্তর d দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ
১) যেকোনো রশ্মি BE থেকে a এর সমান করে BC অংশ কেটে নিই।
২) BC এর C বিন্দুতে x=∠BCF আঁকি।
৩) CF কে CG পর্যন্ত বর্ধিত করি।
৪) CG থেকে d=CD অংশ কেটে নিই।
৫) B, D যোগ করি।
৬) B বিন্দুতে ∠CDB এর সমান করে ∠DBA আঁকি।
৭) BA, DF কে A বিন্দুতে ছেদ করে। তাহলে, △ABC ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, ∠CDB=∠DBA, তাহলে, AB=AD.
∴AB-AC=AD-AC=CD=d; ∠BCA=x; △ABC ই নির্ণেয় ত্রিভুজ।